Understanding Recurrent Neural Networks (RNNs) – part 2 – Day 56
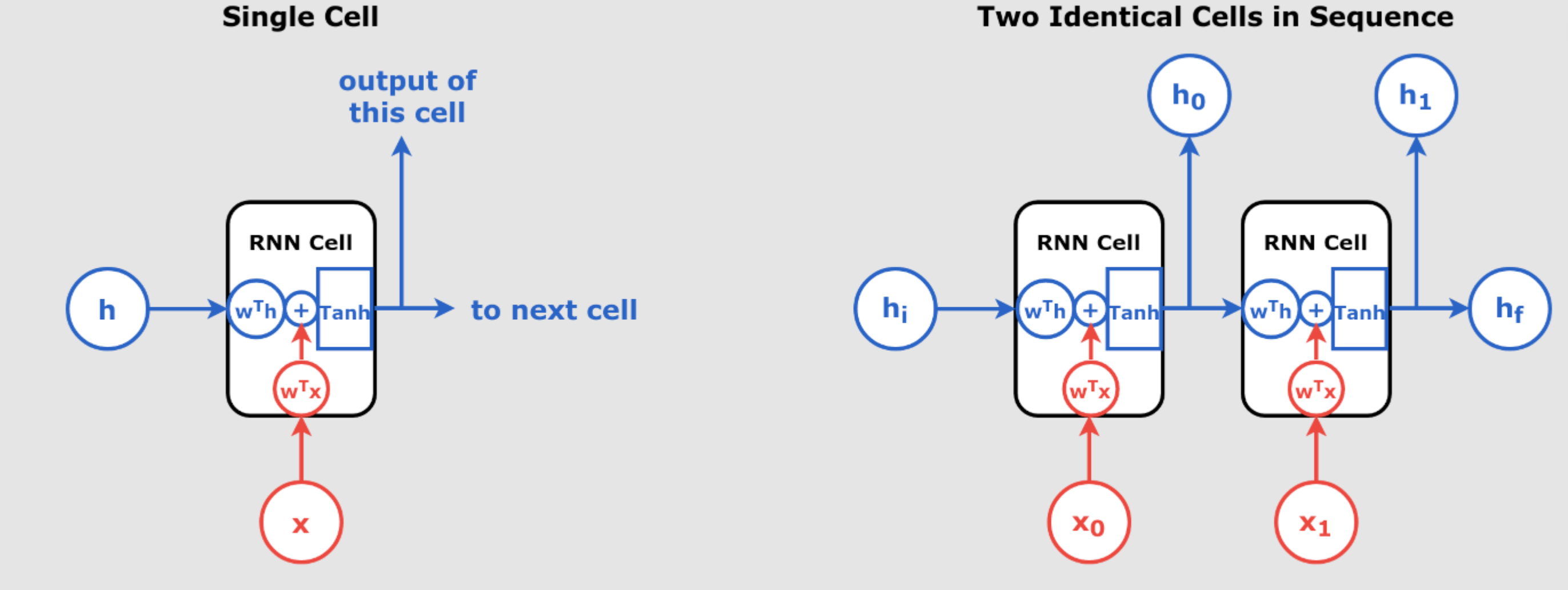
Understanding Recurrent Neural Networks (RNNs) Recurrent Neural Networks (RNNs) are a class of neural networks that excel in handling sequential data, such as time series, text, and speech. Unlike traditional feedforward networks, RNNs have the ability to retain information from previous inputs and use it to influence the current output, making them extremely powerful for tasks where the order of the input data matters. In day 55 article we have introduced RNN. In this article, we will explore the inner workings of RNNs, break down their key components, and understand how they process sequences of data through time. We’ll also...