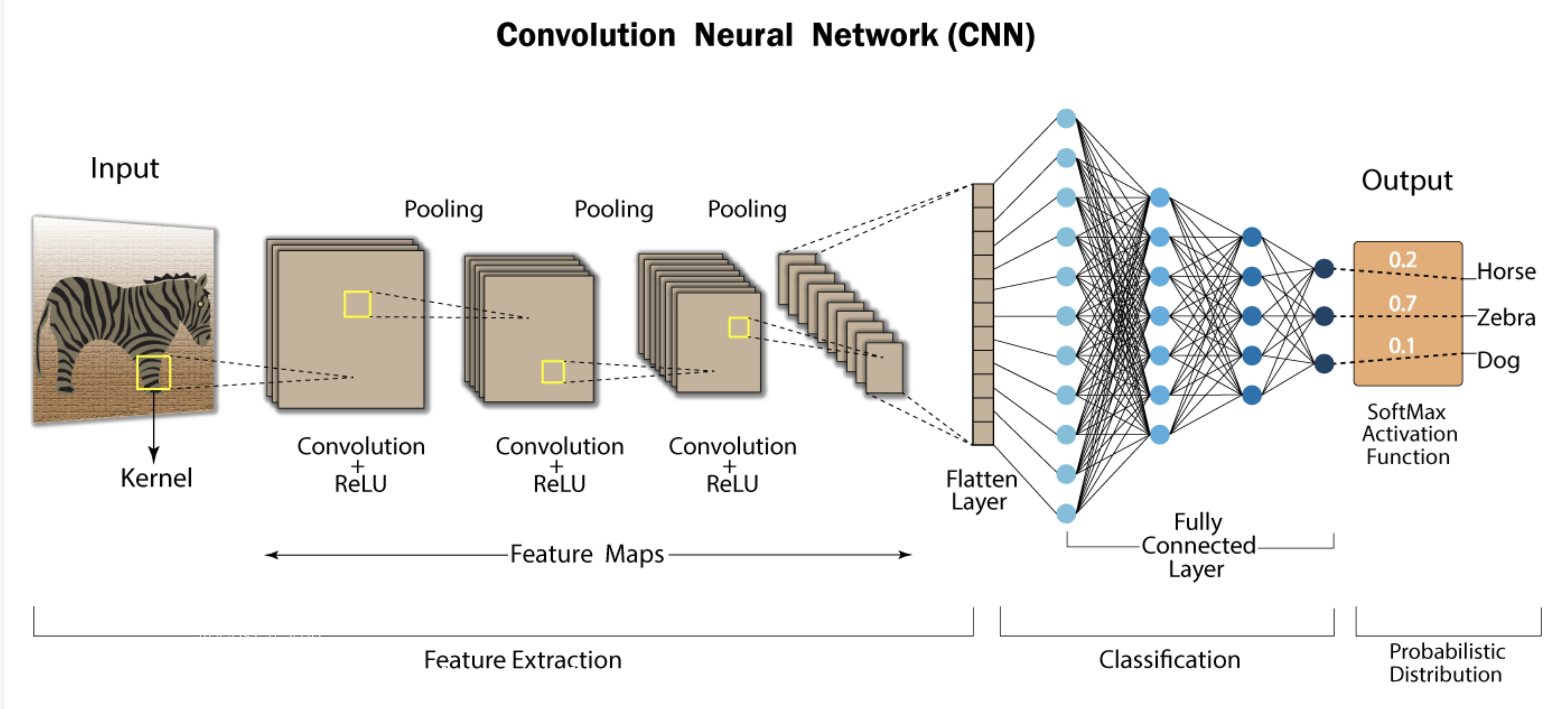
You have seen what CNNs are in our previous article. [View Article] Now, let’s explore the mathematics behind CNNs in detail, step by step, with a very simple example. Part 1: Input Layer, Convolution, and Pooling (Steps 1-4) Step 1: Input Layer We are processing two 3×3 grayscale images—one representing a zebra and one representing a cat. Image 1: Zebra Image (e.g., with stripe-like patterns) Image 2: Cat Image (e.g., with smoother, fur-like textures) These images are represented as 2D grids of pixel values, with each value between 0 and 1 indicating pixel intensity. Step 2: Convolutional Layer (Feature Extraction) We’ll apply a 3×3 convolutional filter to detect patterns such as edges. For simplicity, we’ll use the same filter for both images. Convolution Filter (Edge Detector): Convolution on the Zebra Image For the first patch (the full 3×3 grid), the element-wise multiplication with the filter is: Summing the values: The feature map value for this part of the zebra image is 0.7. Convolution on the Cat Image Now, let’s perform the convolution on the cat image. Summing the values: The feature map value for this part of the cat image is -0.3. Step 3: ReLU Activation (Non-Linearity) The ReLU activation function converts all negative values to 0 while keeping positive values unchanged. Zebra Image (after ReLU): remains 0.7. Cat Image (after ReLU): becomes 0.0. Step 4: Pooling Layer (Downsampling) Next, we apply max pooling to downsample the feature maps. For simplicity, let’s assume we reduce each feature map to a single value: Zebra Image (after pooling): Cat Image (after pooling): Part 2: Fully Connected Layer (Step 5) Now, we move to the fully connected layer, where we combine the features extracted from the convolutional layer and use weights and biases to compute the logits for each class. Step 5: Fully Connected Layer – Weight and Bias Calculation At this point, we’ve flattened the pooled outputs: Zebra Image (flattened): Cat Image (flattened): The fully connected layer computes the logits for each class (zebra, cat) using weights and biases. For this step, we’ll show how weights and biases are applied, and how they are updated based on loss. The formula for the logit of class is: Where: is the weight for class , is the feature value from the previous layer (e.g., ), is the bias for class , is the logit for class (before applying Softmax). Let’s assume the following initial weights and biases for each class: Zebra class: Initial weight: , Initial bias: Cat class: Initial weight: , Initial bias: Logit Calculation for Zebra Image (Flattened Input: [0.7]) For the zebra class: For the cat class: Logit Calculation for Cat Image (Flattened Input: [0.0]) For the zebra class: For the cat class: Part 3: Loss Calculation and Weight/Bias Update (Backpropagation) Now that we’ve computed the logits, we need to calculate the loss and perform backpropagation to update the weights and biases. Loss Calculation (Cross-Entropy Loss) We use cross-entropy loss to measure the difference between the predicted probabilities and the true labels. For simplicity, assume the true label for the zebra image is zebra (1), and the true label for the cat image is cat (1). Cross-entropy loss formula for a single class: Where: is the true label (1 for the correct class, 0 for the others), is the predicted probability for class . First, we apply the Softmax function to convert the logits into probabilities. Softmax for the Zebra Image: Zebra logit: Cat logit: Exponentials: Sum of exponentials: Probabilities: Zebra: Cat: Cross-Entropy Loss for Zebra Image: Let’s assume the true label is “zebra” (1 for zebra, 0 for cat): This is the loss value for the zebra image. Part 4: Weight and Bias Update Using Gradient Descent Using the loss value, the network performs backpropagation to calculate the gradients (partial derivatives of the loss with respect to each weight and bias). These gradients are used to update the weights and biases to reduce the loss in the next iteration. For simplicity, assume the gradients calculated for each weight and bias are as follows (based on chain rule and backpropagation): Gradient for zebra weight: Gradient for zebra bias: Gradient for cat weight: Gradient for cat bias: Updated Weights and Biases Using gradient descent, we update the weights and biases: Where is the learning rate (assume ): For the cat class: Recap The network computes logits using weights and biases. Softmax converts logits into probabilities. Cross-entropy loss measures the error, and gradients are computed through backpropagation. Gradients update the weights and biases to reduce the loss for the next iteration. This entire process repeats until the network minimizes the loss and correctly classifies images of zebras and cats. Part 5: Continuing the Process for Subsequent Iterations Now that we’ve seen how the fully connected layer works and how weights and biases are updated in one iteration, let’s continue to show what happens in the following iterations as the network learns. The goal is to keep refining the weights and biases through backpropagation and gradient descent, so the network gets better at predicting whether the input is a zebra or a cat. Updated Weights and Biases After First Iteration: Zebra class: Updated weight: , Updated bias: Cat class: Updated weight: , Updated bias: Step 5: Fully Connected Layer Calculations for the Second Iteration Logit Calculation for Zebra Image (Flattened Input: [0.7]) Now, using the updated weights and biases, we recalculate the logits for the zebra image. For the zebra class: For the cat class: Logit Calculation for Cat Image (Flattened Input: [0.0]) For the zebra class: For the cat class: Step 6: Reapplying Softmax Function Now, let’s apply the Softmax function to the updated logits to get the new predicted probabilities. For the Zebra Image: Logits: Zebra logit: Cat logit: Exponentials: Sum of exponentials: Probabilities: Zebra: Cat: For the Cat Image: Logits: Zebra logit: Cat logit: Exponentials: Sum of exponentials: Probabilities: Zebra: Cat: Step 7: Recalculating Loss Next, we calculate the cross-entropy loss for both images based on the updated predictions. Loss for Zebra Image: Assume the true label is still “zebra” (1 for zebra, 0 for cat). The cross-entropy loss is: Loss for Cat Image: Assume the true label is still “cat” (0 for zebra, 1 for cat). The cross-entropy loss is: Step 8: Further Weight and Bias Updates Using Backpropagation Now, the network uses backpropagation to compute the gradients again and updates the weights and biases based on the new loss values. For simplicity, assume the gradients for this iteration are as follows: Gradient for zebra weight: Gradient for zebra bias: Gradient for cat weight: Gradient for cat bias: Using gradient descent, the weights and biases are updated again: Similarly, for the cat class: Repeat the Process This process of calculating logits, applying Softmax, calculating loss, and updating weights and biases continues over many iterations until the network minimizes the loss and correctly classifies images with high confidence. Over time, the network improves at distinguishing between zebra and cat features. Input: We started with two images (a zebra and a cat) as input to the CNN. Convolutional Layers: We applied a convolutional filter to detect edge features. ReLU: We applied the ReLU activation function to retain positive feature values. Pooling: We downsampled the feature map using max pooling. Fully Connected Layer: The flattened pooled values were multiplied by weights and added to biases to calculate logits. Softmax: We converted logits into probabilities using the Softmax function. Loss Calculation: We used cross-entropy loss to measure the error between the predicted and true labels. Backpropagation: Gradients were computed, and weights and biases were updated using gradient descent to minimize the loss. Iteration: This process repeated, with weights and biases gradually adjusting to improve classification performance. This detailed process explains how the CNN learns over time to classify images like zebra and cat by adjusting weights and biases based on the loss function! Part 6: Continuing with Next Iteration (Iteration 3) At this point, we’ve already updated the weights and biases after two iterations. Let’s update them again and show how the network refines its predictions as we explained through the repeating the process . Lets show the Updated Weights and Biases After Iteration 2 Zebra class: Updated weight: , Updated bias: Cat class: Updated weight: , Updated bias: Step 5: Fully Connected Layer Calculations for the Next Iteration Logit Calculation for Zebra Image (Flattened Input: [0.7]) For the zebra class: For the cat class: Logit Calculation for Cat Image (Flattened Input: [0.0]) For the zebra class: For the cat class: Step 6: Softmax Calculation (Converting Logits to Probabilities) Next, we apply the Softmax function to convert the logits into probabilities, which will tell us how confident the network is about the image being a zebra or a cat. For the Zebra Image: Logits: Zebra: Cat: Exponentials: Sum of exponentials: Probabilities: Zebra: Cat: For the Cat Image: Logits: Zebra: Cat: Exponentials: Sum of exponentials: Probabilities: Zebra: Cat: Step 7: Final Classification Decision At this point, we have the final probabilities for both the zebra and cat images. For the Zebra Image: The network is 78% confident that the image is a zebra and 22% confident that it’s a cat. Since the probability for zebra is higher, the network classifies the zebra image as a zebra. For the Cat Image: The network is 55% confident that the image is a zebra and 45% confident that it’s a cat. This is a borderline case, but the network leans slightly toward classifying the cat image as a zebra, though with low confidence. Step 8: Improving the Network (More Iterations) At this point, the network still isn’t confident enough about the cat image—the probability for zebra is still higher than for cat. However, the network will continue to update its weights and biases through more iterations to become better at identifying cat-specific features (like smooth textures or fur-like patterns) and distinguishing them from zebra-specific features (like stripes and edges). After many more training iterations, the network will gradually improve its performance and reach higher confidence for classifying both zebras and cats. Over time, the probability for cat in the cat image will rise as the network learns to associate specific patterns with the correct class. Notes The network processes each image through convolutional layers, ReLU, and pooling to extract features. In the fully connected layer, the network uses weights and biases to calculate logits for each class. The Softmax function converts these logits into probabilities, giving the network’s confidence in its predictions. After several iterations of training and weight updates, the network becomes confident that the zebra image is a zebra (with a 78% probability). The network is still unsure about the cat image but leans toward classifying it as a zebra (with 55% probability) due to insufficient training iterations. By continuing the training process (more iterations), the network will eventually be able to classify both images with high confidence, reducing the classification error over time. How the CNN Refines Its Predictions This is how the CNN refines its predictions through the iterative process of backpropagation, weight updates, and loss minimization. With more training and weight adjustment, the network will improve and reduce the classification error for future inputs. As a Perfect Example for CNN integration Check the INGOAMPT app called :background img remove INGOAMPT & Discover how the Ingoampt app leverages CNN deep learning through Apple’s Core ML technology. This is simple app is perfect example of using CNN as a service.Wanna support INGOAMPT? Purchase our Apps to contribute & be part of our journey. Also you can email us at email@ingoampt.comClick Here to Check Our app called Background Remove Image INGOAMPT as a perfect example of CNN & what we explained.. To Understand Deeper, Let’s See Another Example for Math Explanation. with Real Numbers : Lets demystify CNNs by walking through a detailed example using for four simple images this time. We’ll explain each step thoroughly and delve into how the network processes images, makes predictions, and learns over time. The Four-Image Example To make CNNs more accessible, we’ll use a simplified example involving four images and two classes. Classes and Images Classes: Class 0: Cat Class 1: Dog Images: We have four 4×4 grayscale images, each represented as a matrix with pixel values of 0 or 1 for simplicity. Image 1 (Cat): [0, 1, 0, 1] [0, 1, 0, 1] [0, 1, 0, 1] [0, 1, 0, 1] Image 2 (Cat): [1, 1, 1, 1] [0, 0, 0, 0] [1, 1, 1, 1] [0, 0, 0, 0] Image 3 (Dog): [1, 0, 1, 0] [0, 1, 0, 1] [1, 0, 1, 0] [0, 1, 0, 1] Image 4 (Dog): [1, 0, 0, 0] [0, 1, 0, 0] [0, 0, 1, 0] [0, 0, 0, 1] Simplified CNN Architecture Our CNN will consist of the following layers and components: Convolutional Layer: Filters: 2 filters (Filter A and Filter B) Activation Function: ReLU (Rectified Linear Unit) Flattening: Convert feature maps into a feature vector Fully Connected Layer: Output layer with weights and biases Softmax Function: Convert logits into probabilities Loss Function: Cross-entropy loss Training Process: We’ll perform one iteration to demonstrate learning Step-by-Step Processing of the Images We’ll go through each step in detail, explaining how the CNN processes the images, makes predictions, and learns. Step 1: Input Images…
Mastering the Mathematics Behind CNN or Convolutional Neural Networks in Deep Learning – Day 54