Understanding RNNs: Why Not compare it with Feedforward Neural Networks with simple Example to show the Math Behind it ? - DAY 58 INGOAMPT

Understanding RNNs: Why Not compare it with Feedforward Neural Networks with simple Example to show the Math Behind it ? – DAY 58 INGOAMPT

September 28, 2024
Posted by ingoampt

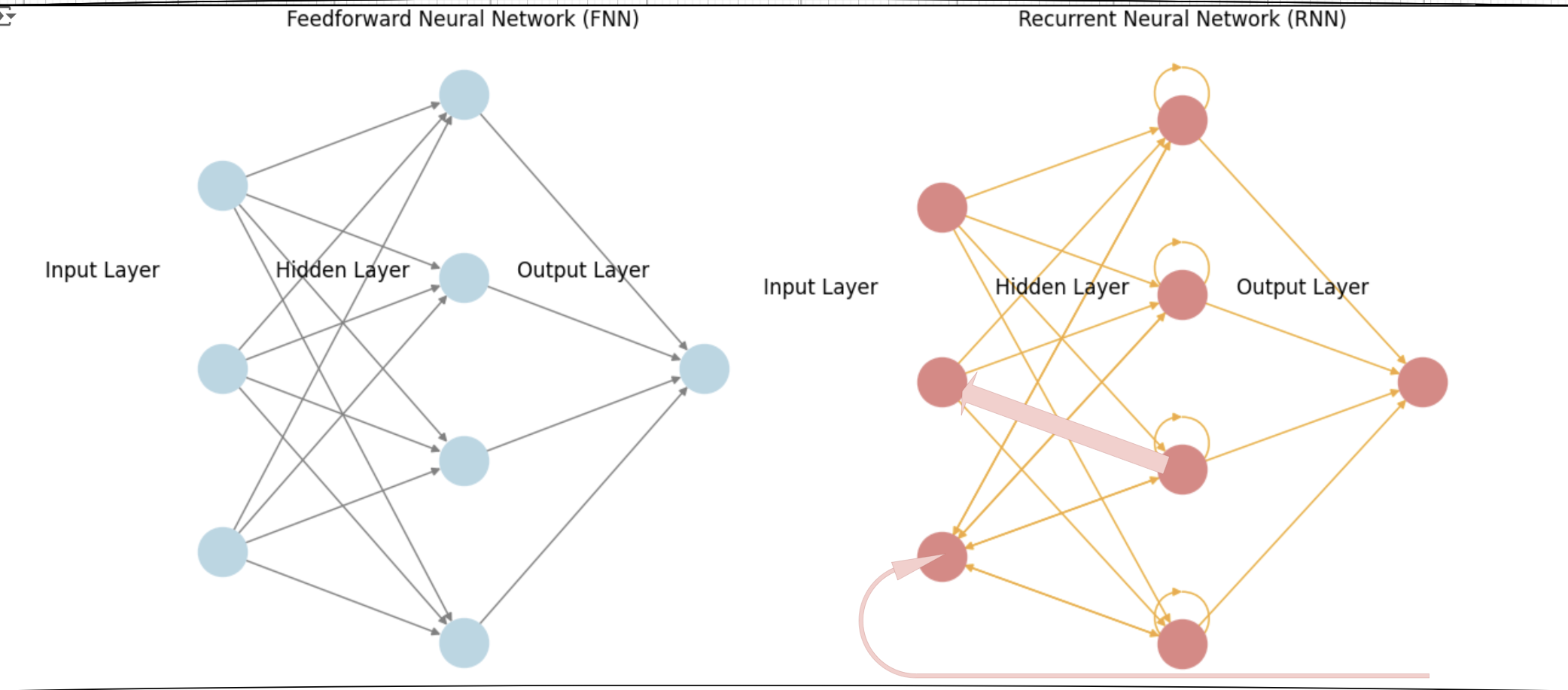
Neural Networks Example

Example Setup

Input for FNN: $x = 0.5$
Target Output for FNN: $y = 0.8$
RNNs are tailored for sequential data because they are designed to remember and utilize information from previous inputs in a sequence, allowing them to capture temporal relationships and context effectively. This characteristic differentiates RNNs from other neural network types that are not inherently sequence-aware., Input for RNN (Sequence): $X = [0.5, 0.7]$
Target Output for RNN (Sequence): $Y = [0.8, 0.9]$
Learning Rate: $\eta = 0.1$

1. Feedforward Neural Network (FNN)

Structure

Input Layer: 1 neuron
Hidden Layer: 1 neuron
Output Layer: 1 neuron

Weights and Biases

Initial Weights:
- $W_{ih} = 0.4$ (Input to Hidden weight)
- $W_{ho} = 0.6$ (Hidden to Output weight)
Biases:
- $b_h = 0.1$ (Hidden layer bias)
- $b_o = 0.2$ (Output layer bias)

Step-by-Step Calculation for FNN

Step 1: Forward Pass

Hidden Layer Output:
$h = \text{ReLU}(W_{ih} \cdot x + b_h) = \text{ReLU}(0.4 \cdot 0.5 + 0.1) = \text{ReLU}(0.2 + 0.1) = \text{ReLU}(0.3) = 0.3$
Output:
$y_{\text{pred}} = W_{ho} \cdot h + b_o = 0.6 \cdot 0.3 + 0.2 = 0.18 + 0.2 = 0.38$

Step 2: Loss Calculation

Using Mean Squared Error (MSE):

$L = \frac{1}{2} (y_{\text{pred}} - y)^2 = \frac{1}{2} (0.38 - 0.8)^2 = \frac{1}{2} (-0.42)^2 = \frac{1}{2} \cdot 0.1764 = 0.0882$

Step 3: Backward Pass

Gradient of Loss with respect to Output:
$\frac{\partial L}{\partial y_{\text{pred}}} = y_{\text{pred}} - y = 0.38 - 0.8 = -0.42$
Gradient of Output with respect to Hidden Layer:
$\frac{\partial y_{\text{pred}}}{\partial h} = W_{ho}$
Gradient of Hidden Layer Output with respect to Weights:
$\frac{\partial L}{\partial W_{ho}} = \frac{\partial L}{\partial y_{\text{pred}}} \cdot \frac{\partial y_{\text{pred}}}{\partial W_{ho}} = -0.42 \cdot 0.3 = -0.126$

$\frac{\partial L}{\partial W_{ih}} = \frac{\partial L}{\partial y_{\text{pred}}} \cdot \frac{\partial y_{\text{pred}}}{\partial h} \cdot \frac{\partial h}{\partial W_{ih}} = -0.42 \cdot W_{ho} \cdot \frac{\partial h}{\partial W_{ih}}$

Assuming $\frac{\partial h}{\partial W_{ih}} = 0.5$ :

$\frac{\partial L}{\partial W_{ih}} = -0.42 \cdot 0.6 \cdot 0.5 = -0.126$

Step 4: Weight Update

Update Output Weight:
$W_{ho} = W_{ho} - \eta \cdot \frac{\partial L}{\partial W_{ho}} = 0.6 - 0.1 \cdot (-0.126) = 0.6 + 0.0126 = 0.6126$
Update Input Weight:
$W_{ih} = W_{ih} - \eta \cdot \frac{\partial L}{\partial W_{ih}} = 0.4 - 0.1 \cdot (-0.126) = 0.4 + 0.0126 = 0.4126$

2. Recurrent Neural Network (RNN)

Structure

Input Layer: 1 neuron
Hidden Layer: 1 neuron
Output Layer: 1 neuron

Weights and Biases

Initial Weights:
- $W_{xh} = 0.5$ (Input to Hidden weight)
- $W_{hh} = 0.3$ (Hidden to Hidden weight)
- $W_{hy} = 0.7$ (Hidden to Output weight)
Biases:
- $b_h = 0.1$ (Hidden layer bias)
- $b_o = 0.2$ (Output layer bias)

Step-by-Step Calculation for RNN

Step 1: Forward Pass

Assuming initial hidden state $h_0 = 0$ . This is where the memory concept starts; the hidden state retains information from previous time steps.

For $t = 1$ (Input $x_1 = 0.5$ ):
- Hidden State:
  $h_1 = \text{tanh}(W_{xh} \cdot x_1 + W_{hh} \cdot h_0 + b_h) = \text{tanh}(0.5 \cdot 0.5 + 0.3 \cdot 0 + 0.1) = \text{tanh}(0.25 + 0.1) = \text{tanh}(0.35) \approx 0.337$
  
  Here, $h_1$ is influenced by the previous hidden state $h_0$ (which is 0). This demonstrates how the RNN maintains memory; the hidden state captures the relevant information to influence future computations.
- Output:
  $y_{1, \text{pred}} = W_{hy} \cdot h_1 + b_o = 0.7 \cdot 0.337 + 0.2 \approx 0.2359 + 0.2 = 0.4359$
For $t = 2$ (Input $x_2 = 0.7$ ):
- Hidden State:
  $h_2 = \text{tanh}(W_{xh} \cdot x_2 + W_{hh} \cdot h_1 + b_h) = \text{tanh}(0.5 \cdot 0.7 + 0.3 \cdot 0.337 + 0.1)$
  
  $= \text{tanh}(0.35 + 0.1011 + 0.1) = \text{tanh}(0.5511) \approx 0.500$
  
  In this step, $h_2$ is influenced by both the current input $x_2$ and the previous hidden state $h_1$ . This reflects the memory of the previous input and its influence on the current state.
- Output:
  $y_{2, \text{pred}} = W_{hy} \cdot h_2 + b_o = 0.7 \cdot 0.500 + 0.2 = 0.35 + 0.2 = 0.55$

Step 2: Loss Calculation

Using Mean Squared Error (MSE) for the sequence:

For $t = 1$ :
$L_1 = \frac{1}{2} (y_{1, \text{pred}} - 0.8)^2 = \frac{1}{2} (0.4359 - 0.8)^2 \approx 0.0613$
For $t = 2$ :
$L_2 = \frac{1}{2} (y_{2, \text{pred}} - 0.9)^2 = \frac{1}{2} (0.55 - 0.9)^2 \approx 0.0600$

Total Loss:

$L_{\text{total}} = L_1 + L_2 \approx 0.0613 + 0.0600 = 0.1213$

Step 3: Backward Pass (BPTT)

This is where backpropagation through time takes place. The gradients are computed considering how each hidden state affects the output across the entire sequence.

Gradient of Loss w.r.t Output:
- For $t = 1$ :
  $\frac{\partial L_1}{\partial y_{1, \text{pred}}} = y_{1, \text{pred}} - 0.8 = 0.4359 - 0.8 = -0.3641$
- For $t = 2$ :
  $\frac{\partial L_2}{\partial y_{2, \text{pred}}} = y_{2, \text{pred}} - 0.9 = 0.55 - 0.9 = -0.35$
Gradient of Output w.r.t Hidden:
$\frac{\partial y_{1, \text{pred}}}{\partial h_1} = W_{hy} = 0.7$

$\frac{\partial y_{2, \text{pred}}}{\partial h_2} = W_{hy} = 0.7$
Gradient of Hidden States:
- For $t = 1$ :
  $\frac{\partial L_1}{\partial h_1} = \frac{\partial L_1}{\partial y_{1, \text{pred}}} \cdot \frac{\partial y_{1, \text{pred}}}{\partial h_1} = -0.3641 \cdot 0.7 = -0.2549$
- For $t = 2$ :
  $\frac{\partial L_2}{\partial h_2} = \frac{\partial L_2}{\partial y_{2, \text{pred}}} \cdot \frac{\partial y_{2, \text{pred}}}{\partial h_2} = -0.35 \cdot 0.7 = -0.245$
- Memory Influence: The hidden state $h_2$ depends on $h_1$ and the current input $x_2$ . Thus, the gradients also account for the memory stored in previous hidden states.
Gradient for Weights:
- For $W_{hy}$ :
  $\frac{\partial L_1}{\partial W_{hy}} = \frac{\partial L_1}{\partial y_{1, \text{pred}}} \cdot h_1 = -0.3641 \cdot 0.337 = -0.122$
- For $W_{hh}$ :
  $\frac{\partial L_2}{\partial W_{hh}} = \frac{\partial L_2}{\partial y_{2, \text{pred}}} \cdot h_1 \cdot W_{hh} = -0.35 \cdot 0.500 \cdot 0.3 = -0.0525$

Step 4: Weight Update

Update Weights:
- For $W_{hy}$ :
  $W_{hy} = W_{hy} - \eta \cdot \frac{\partial L_1}{\partial W_{hy}} = 0.7 - 0.1 \cdot (-0.122) = 0.7 + 0.0122 = 0.7122$
- For $W_{hh}$ :
  $W_{hh} = W_{hh} - \eta \cdot \frac{\partial L_2}{\partial W_{hh}} = 0.3 - 0.1 \cdot (-0.0525) = 0.3 + 0.00525 = 0.30525$

Summary

Feedforward Neural Network (FNN)

Step	Calculation
Forward Pass	$h = 0.3, \; y_{\text{pred}} \approx 0.38$
Loss	$L \approx 0.0882$
Gradient (Output)	$\frac{\partial L}{\partial y_{\text{pred}}} \approx -0.42$
Weight Update	$W_{ho} = 0.6126, \; W_{ih} = 0.4126$

Recurrent Neural Network (RNN)

Step	Calculation	Explanation
Forward Pass	$h_1 \approx 0.337, \; y_{1, \text{pred}} \approx 0.4359$	Hidden state $h_1$ remembers $h_0$ (initial state).
	$h_2 \approx 0.500, \; y_{2, \text{pred}} \approx 0.55$	Hidden state $h_2$ remembers $h_1$ , capturing memory.
Loss	$L_{\text{total}} \approx 0.1213$	Total loss calculated across the sequence.
Gradient (Output)	For $t=1: -0.3641, \; t=2: -0.35$	Gradients computed for each time step output.
Weight Update	$W_{hy} = 0.7122, \; W_{hh} = 0.30525$	Weights updated based on contributions from all previous states.

Key Takeaways

FNN: Each input is treated independently, and the backpropagation process is straightforward.
RNN: The model retains memory of previous states through the hidden state, making the calculations for gradients more complex, especially during backpropagation through time (BPTT). Each hidden state influences subsequent outputs and reflects the model’s ability to remember past inputs.

Another concept to understand here is, memorization in RNNs happens through the hidden states. Each hidden state (h_t) carries information from previous inputs:

At time step $t = 1$ , the hidden state $h_1$ is influenced by the initial hidden state h_0 (which is 0).
At time step $t = 2$ , the hidden state $h_2$ is influenced by both the current input $x_2$ and the previous hidden state $h_1$ .

This shows how RNNs maintain memory of past inputs, but this is short-term memory due to the vanishing gradient problem, where earlier inputs lose influence over time.

Education

Understanding RNNs: Why Not compare it with Feedforward Neural Networks with simple Example to show the Math Behind it ? – DAY 58 INGOAMPT

Neural Networks Example

Example Setup

1. Feedforward Neural Network (FNN)

Structure

Weights and Biases

Step-by-Step Calculation for FNN

Step 1: Forward Pass

Step 2: Loss Calculation

Step 3: Backward Pass

Step 4: Weight Update

2. Recurrent Neural Network (RNN)

Structure

Weights and Biases

Step-by-Step Calculation for RNN

Step 1: Forward Pass

Step 2: Loss Calculation

Step 3: Backward Pass (BPTT)

Step 4: Weight Update

Summary

Feedforward Neural Network (FNN)

Recurrent Neural Network (RNN)

Key Takeaways

don't miss our new posts. Subscribe for updates