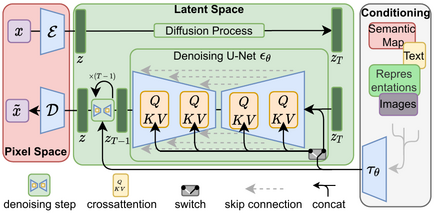
Unveiling Diffusion Models: From Denoising to Generative Art The field of generative modeling has witnessed remarkable advancements over the past few years, with diffusion models emerging as a powerful class capable of generating high-quality, diverse images and other data types. Rooted in concepts from thermodynamics and stochastic processes, diffusion models have not only matched but, in some aspects, surpassed the performance of traditional generative models like Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs). In this blog post, we’ll delve deep into the evolution of diffusion models, understand their underlying mechanisms, and explore their wide-ranging applications and future prospects. Table of Contents Introduction to Diffusion Models Historical Development Understanding Diffusion Models The Forward Diffusion Process (Noising) The Reverse Diffusion Process (Denoising) Training Objective Variance Scheduling Model Architecture Implementing Diffusion Models Applications of Diffusion Models Advancements: Latent Diffusion Models and Beyond Challenges and Limitations Future Directions Conclusion References Additional Resources Introduction to Diffusion Models Diffusion models are a class of probabilistic generative models that learn data distributions by modeling the gradual corruption and subsequent recovery of data through a Markov chain of diffusion steps. The core idea is to learn how to reverse a predefined noising process that progressively adds noise to the data until it becomes indistinguishable from pure noise. By learning this reverse process, the model can generate new data samples starting from random noise. The Conceptual Foundation The inspiration for diffusion models comes from non-equilibrium thermodynamics and stochastic differential equations, particularly the concept of Langevin dynamics. In physics, diffusion processes describe the random movement of particles suspended in a medium, resulting from collisions with the medium’s molecules. Similarly, in diffusion models, data points undergo random perturbations, and the model learns to reverse these perturbations to recover the original data distribution. Historical Development Early Foundations The theoretical foundations of diffusion models date back to earlier works on score matching and denoising autoencoders. In particular, Score Matching, introduced by Aapo Hyvärinen in 2005[1], involves estimating the gradient of the log-density (the score function) of a data distribution, which is central to diffusion models. Formalization of Diffusion Models In 2015, Jascha Sohl-Dickstein et al. formalized diffusion models in their paper “Deep Unsupervised Learning using Nonequilibrium Thermodynamics”[2]. They introduced the concept of modeling the data distribution through a diffusion process and learning to reverse it to generate new data. Although their results were promising, diffusion models didn’t receive significant attention at the time due to the rising popularity of GANs. Breakthrough with DDPM The turning point came in 2020 when Jonathan Ho, Ajay Jain, and Pieter Abbeel introduced Denoising Diffusion Probabilistic Models (DDPMs)[3]. They demonstrated that diffusion models could generate high-fidelity images comparable to those produced by GANs. Their approach involved a refined training objective and an emphasis on the connection between diffusion models and variational inference. Figure 1: Comparison of images generated by GANs and DDPMs To see a comparison between images generated by GANs and DDPMs, refer to Figure 9 in the DDPM paper: “Denoising Diffusion Probabilistic Models” Link: https://arxiv.org/abs/2006.11239 Improvements and Advancements Building upon DDPM, researchers from OpenAI, including Alexander Quinn Nichol and Prafulla Dhariwal, proposed several improvements in their 2021 paper “Improved Denoising Diffusion Probabilistic Models”[4]. They introduced techniques like: Modified Variance Schedules: Adjusting the noise schedule to improve sample quality. Training with Larger Models: Demonstrating that scaling up the model size leads to better results. Hybrid Objectives: Combining different loss functions to enhance training stability and performance. Notable Diffusion Model Papers in 2024 GenPercept and StableNormal: These models introduced single-step diffusion to improve efficiency, focusing on enhancing visual texture and reducing interference during image generation tasks. StableNormal’s two-stage refinement strategy led to high precision in visual details, essential for tasks requiring intricate accuracy. Link: https://ar5iv.org/abs/2409.18124 SiT (Scalable Interpolant Transformers): This model combines flow and diffusion techniques to enhance scalability and sample quality, improving high-resolution image synthesis and adding flexibility to diffusion pathways. By dynamically fine-tuning these pathways, SiT achieves better performance in generative applications. Link: https://ar5iv.org/abs/2401.08740 Lotus: The Lotus model applies diffusion principles to dense prediction tasks, such as monocular depth and surface normal estimation, and employs stochastic methods to predict uncertainty in visual tasks. It effectively maintains detail without increasing model complexity, achieving outstanding results in tasks requiring dense, fine-grained predictions. Link: https://ar5iv.org/abs/2405.12399 Understanding Diffusion Models The Forward Diffusion Process (Noising) The forward process gradually adds noise to the data over \( T \) time steps, transforming an original data sample \( \mathbf{x}_0 \) into a noise vector \( \mathbf{x}_T \). At each time step \( t \), Gaussian noise is added according to: \( q(\mathbf{x}_t | \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 – \beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}) \) \( \beta_t \) is a small positive variance term that controls the amount of noise added at each step. \( \mathbf{I} \) is the identity matrix, ensuring isotropic noise. Table 1: Summary of Notations Symbol Description \( \mathbf{x}_0 \) Original data sample \( \mathbf{x}_t \) Noisy data at time step \( t \) \( \beta_t \) Variance schedule controlling noise addition \( \alpha_t \) Defined as \( 1 – \beta_t \) \( \bar{\alpha}_t \) Cumulative product \( \prod_{s=1}^{t} \alpha_s \) An important property is that we can sample \( \mathbf{x}_t \) at any time step directly from \( \mathbf{x}_0 \) using the closed-form solution: \( q(\mathbf{x}_t | \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 – \bar{\alpha}_t) \mathbf{I}) \) This property allows efficient computation without iterating through all intermediate steps. Figure 2: Visualization of the Forward Diffusion Process For a visual explanation of how noise is added over time, see Figure 2 in the blog post “An Introduction to Diffusion Models for Machine Learning” on Lil’Log: Understanding Diffusion Models The Reverse Diffusion Process (Denoising) The reverse process aims to recover \( \mathbf{x}_0 \) from \( \mathbf{x}_T \) by iteratively removing noise: \( p_\theta(\mathbf{x}_{t-1} | \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \mu_\theta(\mathbf{x}_t, t), \Sigma_\theta(\mathbf{x}_t, t)) \) Training Objective The training objective derives from variational inference and can be simplified to a weighted sum of denoising score matching losses at each time step: \( L = \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}, t} \left[ \left\| \boldsymbol{\epsilon} – \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \right\|^2 \right] \) Variance Scheduling The variance schedule \( \beta_t \) plays a crucial role in the model’s performance. Common choices include linear schedules, but later works have proposed cosine schedules[4] and learned schedules for better results. For example, the cosine schedule is defined as: \( \bar{\alpha}_t = \frac{f(t)}{f(0)} \quad \text{where} \quad f(t) = \cos\left( \frac{t / T + s}{1 + s} \cdot \frac{\pi}{2} \right)^2 \) The Reverse Sampling Equation The update equation for one reverse diffusion step is: \( \mathbf{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{x}_t – \frac{1 – \alpha_t}{\sqrt{1 – \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \right) + \sigma_t \mathbf{z} \) \( \sigma_t \) is a variance term, often set to \( \sqrt{\beta_t} \). \( \mathbf{z} \) is standard Gaussian noise. Model Architecture U-Net Backbone The most successful diffusion models utilize a U-Net architecture[5] as the backbone for \( \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \). The U-Net is an encoder-decoder network with skip connections, allowing it to capture both global and local features efficiently. Downsampling Path: Extracts features at multiple scales. Upsampling Path: Reconstructs the image while integrating features from the downsampling path via skip connections. Figure 5: U-Net Architecture To see an illustration of the U-Net architecture, refer to Figure 1 in the original U-Net paper: “U-Net: Convolutional Networks for Biomedical Image Segmentation” Link: https://arxiv.org/abs/1505.04597 Incorporating Time Steps Positional Encoding: Similar to Transformers, the scalar time \( t \) is transformed into a higher-dimensional vector using sinusoidal functions. Learned Embeddings: Alternatively, \( t \) can be embedded using learned embeddings passed through embedding layers. Attention Mechanisms Some diffusion models incorporate attention mechanisms, such as multi-head self-attention, to capture long-range dependencies in the data. This is particularly beneficial for high-resolution images where global coherence is important. Implementing Diffusion Models Data Preparation: Normalize data to have zero mean and unit variance. Compute the variance schedule \( \beta_t \) and cumulative products \( \bar{\alpha}_t \). Model Definition: Use a U-Net architecture with appropriate modifications. Incorporate time embeddings. Training Loop: For each batch: Sample random \( t \) and noise \( \boldsymbol{\epsilon} \). Generate \( \mathbf{x}_t \) using the forward process. Compute the loss between \( \boldsymbol{\epsilon} \) and \( \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \). Optimize the model parameters using the chosen optimizer. Sampling (Generation): Start from \( \mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \). Iteratively apply the reverse process to obtain \( \mathbf{x}_{t-1} \) from \( \mathbf{x}_t \). After \( T \) steps, obtain \( \mathbf{x}_0 \), a generated data sample. Algorithm 1: Pseudocode for Training and Sampling # Training for each epoch: for each batch of data x0: t ~ Uniform(1, T) ε ~ N(0, I) xt = sqrt(ᾱ_t) * x0 + sqrt(1 – ᾱ_t) * ε Loss = ||ε – εθ(xt, t)||^2 Backpropagate and update θ # Sampling xT ~ N(0, I) for t from T to 1: z ~ N(0, I) if t > 1 else 0 x_{t-1} = (1 / sqrt(α_t)) * (xt – (1 – α_t) / sqrt(1 – ᾱ_t) * εθ(xt, t)) + σ_t * z xt = x_{t-1} For a detailed implementation guide, you can refer to the blog post by Hugging Face: “Diffusion Models: A Practical Guide” Link: https://huggingface.co/blog/annotated-diffusion Applications of Diffusion Models Image Generation Diffusion models have been successful in generating high-resolution, high-fidelity images across various datasets, including: ImageNet: Generating diverse images conditioned on class labels. Face Generation: Producing realistic human faces. Figure 6: Images Generated by Diffusion Models You can view samples of images generated by diffusion models in the official OpenAI blog post: “Cascaded Diffusion Models for High-Resolution Image Synthesis” Link: https://openai.com/blog/diffusion-models/ Text-to-Image Synthesis By conditioning the diffusion process on text embeddings (e.g., from a language model), diffusion models can generate images from textual descriptions. This has led to models like: DALL·E 2: Developed by OpenAI, combining CLIP embeddings with diffusion models[6]. Imagen: From Google Research, utilizing large language models for text conditioning[7]. Figure 7: Text-to-Image Generation Examples Explore examples of text-to-image synthesis on the OpenAI DALL·E 2 page: “DALL·E 2 Examples” Link: https://openai.com/dall-e-2/ Audio and Speech Generation Diffusion models have been adapted for audio synthesis, including: WaveGrad: For generating raw audio waveforms[8]. DiffWave: For text-to-speech applications[9]. Figure 8: Audio Waveform Generation Listen to audio samples generated by WaveGrad on their GitHub repository: “WaveGrad Audio Samples” Link: https://github.com/lmnt-com/wavegrad Molecular Generation In computational chemistry and drug discovery, diffusion models can generate novel molecular structures with desired properties[10]. Figure 9: Molecules Generated by Diffusion Models For examples of molecule generation, refer to the paper “Score-Based Generative Modeling in Latent Space” and its associated GitHub repository: “Molecule Generation Examples” Link: https://github.com/yang-song/score_flow Super-Resolution and Inpainting Diffusion models can enhance image resolution and fill in missing or corrupted parts of images, leveraging their strong generative capabilities. Figure 10: Image Super-Resolution with Diffusion Models See examples of super-resolution in the paper “Enhanced Super-Resolution through Attention to Texture and Structure” Link: https://arxiv.org/abs/2102.01691 Advancements: Latent Diffusion Models and Beyond Latent Diffusion Models (LDMs) To address the computational challenges of operating in high-dimensional data spaces, Latent Diffusion Models[11] perform diffusion in a lower-dimensional latent space learned by an autoencoder. Autoencoder Framework: Encoder: Compresses data into latent representations. Decoder: Reconstructs data from latent space. Diffusion in Latent Space: Reduces computational load and accelerates sampling. Figure 11: Latent Diffusion Model Framework For an in-depth explanation and visualizations, refer to the Latent Diffusion Models paper: “High-Resolution Image Synthesis with Latent Diffusion Models” Link: https://arxiv.org/abs/2112.10752 Stable Diffusion Stable Diffusion[12] is a prominent example of an LDM that has been open-sourced, providing powerful text-to-image generation capabilities. It leverages: Efficient Training: By operating in latent space, training becomes more feasible on limited hardware. Flexible Conditioning: Supports conditioning on text prompts, images, and other modalities. Figure 12: Images Generated by Stable Diffusion Explore a gallery of images generated by Stable Diffusion on their official website: “Stable Diffusion Showcase” Link: https://stability.ai/stablediffusion Accelerating Sampling A major focus has been reducing the number of diffusion steps required for generation, leading to faster sampling times. Techniques include: Denoising Diffusion Implicit Models (DDIM): Deterministic sampling methods that require fewer steps[13]. Knowledge Distillation: Training smaller models to mimic larger ones in fewer steps. Challenges and Limitations While diffusion models have shown great promise, they come with challenges: Computational Cost: Training and sampling can be resource-intensive, especially for high-resolution data. Model Complexity: The need for large models and careful tuning of hyperparameters. Sampling Speed: Even with improvements, generating samples can be slower compared to GANs. Interpretability: Understanding the internal workings and decision-making process is non-trivial. Future Directions The research community is actively exploring ways to: Enhance Efficiency: Developing algorithms for faster sampling and more efficient training. Extend Modalities: Applying diffusion models to other data types like video, 3D models, and more. Improve Control: Allowing finer control over generated outputs through better conditioning methods. Integrate with Other Models: Combining diffusion models with other architectures like Transformers for synergistic effects. Theoretical Understanding: Deepening the theoretical foundations to better understand why diffusion models perform so well. Practical Example for Diffusion Model: Understanding Through Code This example is ideal for anyone aiming to grasp the core concepts of diffusion models through practical application, as it guides you from setting up the variance schedule to generating images with the reverse diffusion process. 1. Variance Schedule: Controlling the Diffusion Process The diffusion process gradually adds noise to an image until it is unrecognizable. By…
Breaking Down Diffusion Models in Deep Learning – Day 75