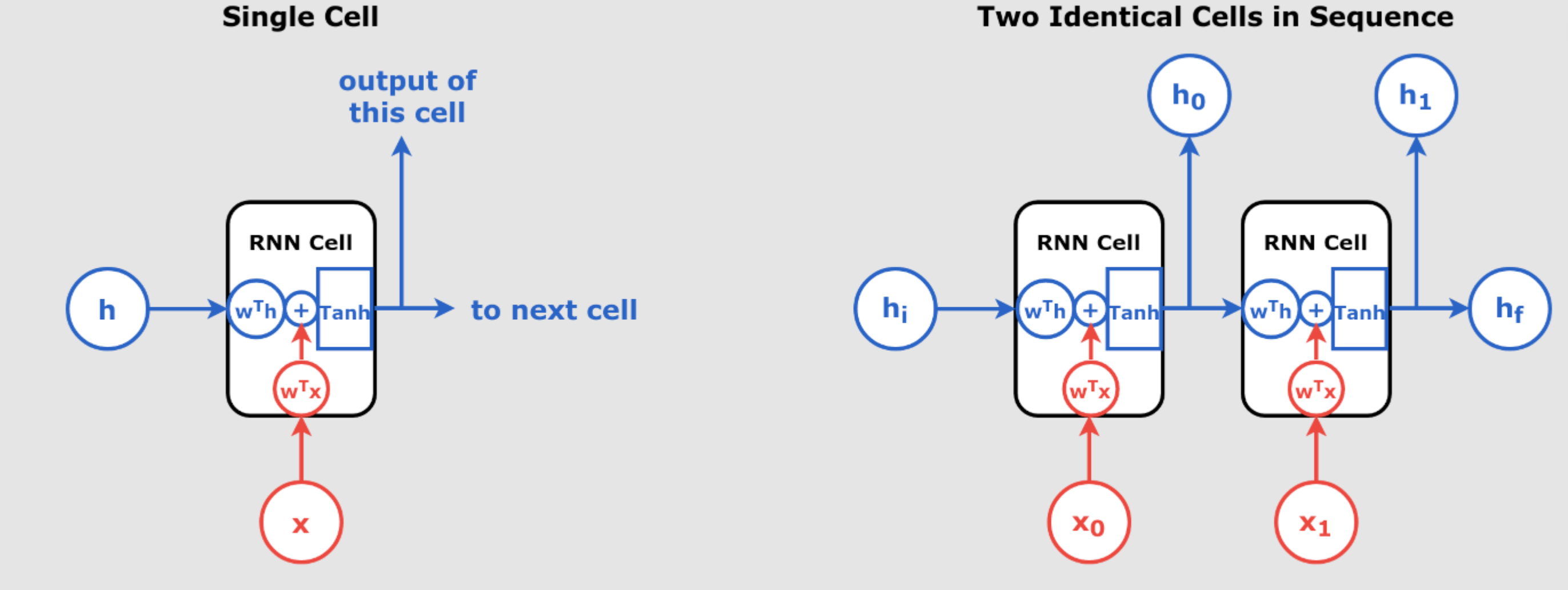
Mastering Time Series Forecasting with RNNs and Seq2Seq Models: Detailed Iterations with Calculations, Tables, and Method-Specific Features Time series forecasting is a crucial task in various domains such as finance, weather prediction, and energy management. Recurrent Neural Networks (RNNs) and Sequence-to-Sequence (Seq2Seq) models are powerful tools for handling sequential data. In this guide, we will provide step-by-step calculations, including forward passes, loss computations, and backpropagation for two iterations across three forecasting methods: Iterative Forecasting: Predicting One Step at a Time Direct Multi-Step Forecasting with RNN Seq2Seq Models for Time Series Forecasting Assumptions and Initial Parameters For consistency across all methods, we’ll use the following initial parameters: Input Sequence: Desired Outputs: For Iterative Forecasting and Seq2Seq: For Direct Multi-Step Forecasting: Initial Weights and Biases: Weights: (hidden-to-hidden weight) (input-to-hidden weight) will vary per method to accommodate output dimensions. Biases: Activation Function: Hyperbolic tangent () Learning Rate: Initial Hidden State: 1. Iterative Forecasting: Predicting One Step at a Time In iterative forecasting, the model predicts one time step ahead and uses that prediction as an input to predict the next step during inference. Key Feature: During training, we use actual data to prevent error accumulation, but during inference, predictions are fed back into the model. Iteration 1 Forward Pass We compute the hidden states and outputs for each time step. Time Step 110220.291330.569 Feature Highlight: Each hidden state depends on the previous hidden state and the current input , showcasing the sequential processing of RNNs. Loss Calculation Compute the Mean Squared Error (MSE): Time Step 10.291220.569330.7554TotalSum = 19.337MSE Backpropagation Feature Highlight: We use Backpropagation Through Time (BPTT) to compute gradients over the entire sequence, considering temporal dependencies. Step 1: Gradients w.r.t Outputs Time Step 10.291220.569330.7554 Step 2: Gradients w.r.t and Compute: Feature Highlight: Gradients for the output layer accumulate over time steps, reflecting the influence of each time step on the loss. Step 3: Gradients w.r.t Hidden States Starting from the last time step and moving backward. At : Compute: Feature Highlight: The derivative of the activation function is used because of the tanh activation. At : Compute: At : Compute: Feature Highlight: Gradients w.r.t hidden states consider both the direct error at the current time step and the propagated error from future time steps. Step 4: Gradients w.r.t , , and Compute: Calculations: For : For : For : Feature Highlight: Gradients for weights are influenced by both inputs and hidden states, showing how the network learns from the sequence data. < Mastering Time Series Forecasting with RNNs and Seq2Seq Models Step 5: Update Weights and Biases Update parameters using gradient descent: \[ W_y^{\text{new}} = W_y – \eta \frac{\partial L}{\partial W_y} = 1.0 – 0.01 \times (-4.326) = 1.043 \] \[ b_y^{\text{new}} = b_y – \eta \frac{\partial L}{\partial b_y} = 0.0 – 0.01 \times (-7.385) = 0.074 \] \[ W_h^{\text{new}} = W_h – \eta \frac{\partial L}{\partial W_h} = 0.5 – 0.01 \times (-1.410) = 0.514 \] \[ W_x^{\text{new}} = W_x – \eta \frac{\partial L}{\partial W_x} = 0.2 – 0.01 \times (-10.945) = 0.309 \] \[ b_h^{\text{new}} = b_h – \eta \frac{\partial L}{\partial b_h} = 0.1 – 0.01 \times (-6.041) = 0.161 \] Feature Highlight: Parameters are updated based on accumulated gradients, improving the model’s predictions in subsequent iterations. Iteration 2 Using updated parameters. Forward Pass Time Step 110220.438330.759 Feature Highlight: Updated parameters result in different activations and outputs, reflecting the learning process. Loss Calculation Time Step 10.530220.866331.0194TotalSum = 15.586MSE Feature Highlight: The decrease in loss indicates that the model is learning and improving its predictions. Backpropagation Repeat the same backpropagation steps as in Iteration 1, using the updated parameters.. 2. Direct Multi-Step Forecasting with RNN In direct multi-step forecasting, the model predicts multiple future time steps simultaneously using the final hidden state of the RNN, without feeding predictions back into the model. Key Feature: The model outputs multiple predictions at once, capturing dependencies between future steps directly, and backpropagation occurs through the final hidden state to the input time steps. Iteration 1 Forward Pass We process the input sequence to obtain the final hidden state and then predict multiple future outputs. Time Step 110220.291330.569 Feature Highlight: Unlike iterative forecasting, we only compute outputs after processing the entire input sequence, using the final hidden state . Predict Outputs: Assuming is adjusted to output two values: Let be a matrix: Compute the predictions: Feature Highlight: The model predicts multiple future steps simultaneously from the final hidden state. Loss Calculation Compute the Mean Squared Error (MSE): Output Index 10.755420.6045TotalSum = 29.839MSE Backpropagation Feature Highlight: Backpropagation flows from the outputs back through the final hidden state and then through the time steps, without iterative feedback from predictions. Step 1: Gradients w.r.t Outputs Compute: Step 2: Gradients w.r.t and Feature Highlight: The gradient w.r.t is calculated using the final hidden state and the errors from both outputs. Step 3: Gradient w.r.t Final Hidden State Compute derivative through the activation function: Feature Highlight: The error is backpropagated from both outputs to the final hidden state, reflecting the simultaneous prediction of multiple steps. Step 4: Backpropagate to Previous Time Steps Compute for and : At : At : Feature Highlight: Gradients are propagated back through time steps from the final hidden state without considering future predicted outputs. Step 5: Gradients w.r.t , , and Compute: For : For : For : Feature Highlight: Weight gradients are computed based on the backpropagated errors from the final hidden state through the RNN layers. Step 6: Update Weights and Biases Update parameters: Feature Highlight: Parameters are updated based on gradients that reflect the simultaneous prediction of future steps. Iteration 2 Forward Pass Time Step 110220.425330.765 Predict Outputs Loss Calculation Output Index 11.000420.8075TotalSum = 26.550MSE Feature Highlight: The loss has decreased compared to the first iteration, indicating learning progress. Backpropagation Repeat the backpropagation steps as in Iteration 1, using updated parameters and calculations. 3. Seq2Seq Models for Time Series Forecasting Seq2Seq models use an encoder-decoder architecture to handle input and output sequences of different lengths. Key Feature: The model consists of two separate RNNs: an encoder that processes the input sequence and a decoder that generates the output sequence, allowing flexible sequence lengths and capturing complex temporal dependencies. Iteration 1 Forward Pass Encoder Process input sequence to obtain the final hidden state . Encoder Time Step 110220.291330.569 Decoder Initialize decoder hidden state . Assuming teacher forcing, we use the actual previous output as input. Decoder Weights: We’ll use separate weights for the decoder: Feature Highlight: The encoder and decoder have separate parameters, allowing for different dynamics in processing inputs and generating outputs. Decoder Time Step 10 (start token)0.755220.503330.717 Feature Highlight: The decoder uses the encoder’s final hidden state as its initial hidden state and processes the target sequence (using teacher forcing). Loss Calculation Compute the MSE over the decoder outputs: Time Step 10.503220.717330.8374TotalSum = 17.461MSE Backpropagation Feature Highlight: Backpropagation involves computing gradients through both the decoder and encoder, considering their separate parameters and the dependency of the decoder’s initial state on the encoder’s final state. Step 1: Gradients w.r.t Decoder Outputs Compute: Step 2: Backpropagation Through Decoder Time Steps Compute gradients w.r.t decoder weights and biases. At : At : At : Feature Highlight: Errors are backpropagated through the decoder time steps, and gradients are computed for decoder-specific weights and biases. Step 3: Gradients w.r.t Decoder Weights and Biases Compute: For : Total: For : Total: For : Total: For : Feature Highlight: Separate gradients are computed for the decoder’s weights and biases, independent of the encoder. Step 4: Gradient w.r.t Encoder’s Final Hidden State Since , we need to compute: Step 5: Backpropagation Through Encoder Time Steps Compute for encoder time steps : At : At : At : Feature Highlight: The encoder receives gradients backpropagated from the decoder, allowing the encoder to adjust its parameters based on the decoder’s performance. Step 6: Gradients w.r.t Encoder Weights and Biases Compute: For : For : For : Feature Highlight: The encoder’s parameters are updated based on how well the decoder performs, enabling the entire Seq2Seq model to learn jointly. Iteration 2 Using updated parameters, repeat the forward pass and backpropagation steps for both the encoder and decoder. Overall Feature Highlight: Seq2Seq models allow for flexible input and output sequence lengths, with separate encoder and decoder networks learning jointly. The backpropagation process involves gradients flowing from the decoder outputs back through the decoder and then to the encoder, enabling complex temporal dependencies to be captured. By providing detailed calculations, tables, and highlighting method-specific features during the calculations, we’ve covered the 3 methods: Iterative Forecasting which is Predicting One Step at a Time and Direct Multi-Step Forecasting with RNN and Seq2Seq Models for Time Series Forecasting, demonstrating how each method processes data differently and how backpropagation is performed uniquely in each case. Key Notes: Time Series Forecasting Methods Comparison Here is a more detailed comparison of the three time series forecasting methods, including which is likely to have less error and insights into their current popularity based on 2024 trends. Complete Table Comparing the Forecasting Methods MethodPrediction StyleWhen to UseDrawbacksExample Use CaseError PropensityPopularity in 2024Iterative ForecastingPredicts one step at a timeWhen future depends on the immediate past (short-term)Error accumulation due to feedbackStock prices or energy consumption predictionHigh error potential (due to error feedback)Commonly used for simple tasksDirect Multi-Step ForecastingPredicts multiple steps at onceWhen future steps are loosely connected (medium-term)May miss time step dependenciesSales forecasting for the next few monthsModerate error, but no feedback loop errorsModerate use, effective for medium-termSeq2Seq ModelsEncoder-decoder for full sequenceFor long-term predictions or variable-length sequencesMore complex and harder to trainLong-term financial forecasts or weather predictionsLower error for complex or long-term tasksIncreasingly popular for complex forecasting, especially in deep learning Text-Based Graph Representations for Each Method 1. Iterative Forecasting (Predicting One Step at a Time) This method predicts one step at a time and uses the predicted output as input for the next step, introducing a feedback loop. Input: [X₁, X₂, X₃] —> Y₁ | | v v Next Input: [X₂, X₃, Y₁] —> Y₂ | | v v Next Input: [X₃, Y₁, Y₂] —> Y₃ Error Propensity: As each prediction is used in the next step, errors from one prediction propagate through subsequent steps, leading to higher cumulative error. 2. Direct Multi-Step Forecasting with RNN This method predicts multiple future steps at once, based on the input sequence, without any feedback loop. Input: [X₁, X₂, X₃] —> [Y₁, Y₂, Y₃] Error Propensity: The model outputs multiple predictions at once, which can lead to moderate error, but avoids feedback loop problems. 3. Seq2Seq Models for Time Series Forecasting Seq2Seq models use an encoder-decoder architecture, where the encoder processes the input sequence into a context vector, and the decoder generates the future sequence. Encoder: [X₁, X₂, X₃] —> Context Vector —> Decoder: [Y₁, Y₂, Y₃] Error Propensity: This model has lower error when applied to complex and long-term time series forecasting problems, as it captures dependencies across the entire sequence. Still not clear ? We know it sounds complicated at first , Therefore, Lets explain another way : Part 1: Iterative Forecasting (One Step at a Time) Training Process The model predicts one time step ahead and feeds that prediction as input for the next step. Example Input: [1, 2, 3] → Predicted Output (during training): [2, 3, 4] Inference Process During inference, the model predicts unseen future values based on new inputs. Example Input: [3, 4, 5] → Predicted Output (during inference): [6, 7] Loss Calculation The model calculates the error between the predicted value and the actual target: The total loss is summed over all predictions. Backpropagation & Weight Updates After each time step, the model uses Backpropagation Through Time (BPTT) to calculate the gradients and update the weights: Where is the learning rate, and is the gradient of the loss. Graph Representation Training: Input: [1, 2, 3] —> Y₁ = 2 Calculate Loss —> Update weights for Y₁ | v Next Input: [2, 3, Y₁] —> Y₂ = 3 Calculate Loss —> Update weights for Y₂ | v Next Input: [3, Y₁, Y₂] —> Y₃ = 4 Calculate Loss —> Update weights for Y₃ Inference: Input: [3, 4, 5] —> Model predicts Y₁ = 6, Y₂ = 7 Error Accumulation Since each prediction depends on the previous step’s prediction, any errors from one prediction will propagate forward, leading to higher loss over time. Pros Useful for short-term predictions where immediate dependencies exist between time steps. Cons Error accumulation: If the early predictions are wrong, subsequent steps are affected, which increases the overall error. Part 2: Direct Multi-Step Forecasting Training Process The model predicts multiple future values at once without feeding the predictions back into the input. Example Input: [1, 2, 3] → Predicted Output: [4, 5] Inference Process In inference, the model predicts multiple future values based on the new unseen input. Example Input: [3, 4, 5] → Predicted Output: [6, 7] Loss Calculation The loss is calculated simultaneously for all predictions: Backpropagation & Weight Updates The model adjusts its weights after all predictions are made: Graph Representation Training: Input: [1, 2, 3] —> Y₁ = 4, Y₂ = 5 Calculate Total Loss (for Y₁ and Y₂) —> Update weights Inference: Input: [3, 4, 5] —> Model predicts Y₁ = 6, Y₂ = 7 No Error Accumulation Since all future steps are predicted at once, there is no error propagation between predictions, which can result in more accurate predictions. Pros Suitable for medium-term forecasting tasks where multiple predictions are needed at once. Avoids the issue of feedback loops. Cons It may miss some time dependencies between individual time steps, especially if they are strongly connected. Part 3: Seq2Seq Models (Encoder-Decoder Architecture) Training Process The model uses an encoder-decoder structure, where the encoder processes the input sequence into a context vector, and the decoder generates the output sequence based on that vector. Example Input: [1, 2, 3] → Predicted Output: [4, 5] Inference Process The model predicts unseen future values based on new inputs and the context vector generated by the encoder. Example Input: [3, 4, 5] → Predicted Output: [6, 7] Loss Calculation The total loss is calculated across all predicted outputs: Backpropagation & Weight Updates The model uses Backpropagation Through Time (BPTT) to update the weights in both the encoder and decoder: Graph Representation Training: Encoder: [1, 2, 3] —> Context Vector | v Decoder: Context Vector —> Y₁ = 4, Y₂ = 5 Calculate Total Loss —> Update weights for encoder and decoder Inference: Encoder: [3, 4, 5] —> Model predicts Y₁ = 6, Y₂ = 7 Long-Term Dependencies The Seq2Seq architecture is highly effective at capturing long-term dependencies between input and output sequences. The context vector provides a summary of the entire input, allowing for more accurate predictions over longer time horizons. Pros Best for long-term forecasting, especially when there are complex relationships between different time steps. The encoder-decoder structure is powerful in handling variable-length sequences. Cons Requires more computational resources due to its complexity. May need more training data to perform well. Final Thoughts: Choosing the Best Method Each forecasting method has its strengths and weaknesses: Iterative Forecasting: Ideal for short-term predictions where there are immediate dependencies between the time steps, but it suffers from error accumulation, which can lead to higher overall loss over time. Direct Multi-Step Forecasting: This method avoids error feedback by predicting all future steps simultaneously, making it more suitable for medium-term forecasting. However, it might miss dependencies between individual time steps if the time steps are strongly connected. Seq2Seq Models: Best for long-term predictions where each future step depends on the entire input sequence. The encoder-decoder architecture is powerful for complex and variable-length sequences but requires more computational resources and data to achieve good performance. Which Method Decreases Loss Better? In summary, the method that decreases loss better depends on the forecasting task: Iterative Forecasting: Works well for short-term forecasting but suffers from error propagation. Direct Multi-Step Forecasting: Effective when you need to predict multiple steps at once without feedback loops. However, it may miss subtle time dependencies. Seq2Seq Models: Generally offer better performance in long-term forecasting because they capture complex dependencies across the entire input sequence. This helps reduce loss for complex tasks, but they require more training data and computational power. Final Recommendation Choosing the right forecasting method depends on the task at hand: If you are predicting short-term sequences with immediate dependencies, use Iterative Forecasting. If you need multiple steps predicted at once without worrying about feedback loops, opt for Direct Multi-Step Forecasting. If you’re working with long-term forecasts and complex relationships between inputs and outputs, the Seq2Seq Model will likely be the best choice. Now is Time for Coding Part 1: Iterative Forecasting (One Step at a Time) Example: Input Sequence: [1, 2, 3] Target Sequence (during training): [4] (the next time step) Explanation: One-Step Prediction: The model is trained to predict the next time step based on the input sequence. Iterative Inference: During inference (testing), the model uses its previous predictions as input to predict subsequent steps. Key Difference: The model outputs a single value at each step, making predictions iteratively for multi-step forecasting. PyTorch Code Example import torch import torch.nn as nn import torch.optim as optim # Define the RNN model for Iterative Forecasting class IterativeRNN(nn.Module): def __init__(self, input_size, hidden_size, output_size): super(IterativeRNN, self).__init__() self.rnn = nn.RNN(input_size, hidden_size, batch_first=True) self.fc = nn.Linear(hidden_size, output_size) # Predicts one time step ahead def forward(self, x, hidden): # Pass input through RNN layer out, hidden = self.rnn(x, hidden) # Output only the last time step for prediction out = self.fc(out[:, -1, :]) return out, hidden # Hyperparameters input_size = 1 # Feature dimension hidden_size = 10 # Number of hidden units output_size = 1 # Predicting one value learning_rate = 0.01 num_epochs = 100 # Training data x_train = torch.tensor([[[1.0], [2.0], [3.0]]]) # Shape: (batch_size, seq_length, input_size) y_train = torch.tensor([[4.0]]) # Shape: (batch_size, output_size) # Initialize the model, loss function, and optimizer model = IterativeRNN(input_size, hidden_size, output_size) criterion = nn.MSELoss() # Mean Squared Error for regression tasks optimizer = optim.Adam(model.parameters(), lr=learning_rate) # Training loop for epoch in range(num_epochs): model.train() optimizer.zero_grad() # Reset gradients hidden = torch.zeros(1, x_train.size(0), hidden_size) # Initialize hidden state output, hidden = model(x_train, hidden) # Forward pass loss = criterion(output, y_train) # Calculate loss loss.backward() # Backpropagation optimizer.step() # Update weights if (epoch + 1) % 10 == 0: print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}') # Inference: Predicting future values iteratively model.eval() with torch.no_grad(): input_seq = x_train.clone() # Start with the training input hidden = torch.zeros(1, input_seq.size(0), hidden_size) # Initialize hidden state num_predictions = 2 # Number of future steps to predict predictions = [] for _ in range(num_predictions): output, hidden = model(input_seq, hidden) # Predict next step predictions.append(output.item()) # Save prediction # Update input sequence by appending the prediction input_seq = torch.cat((input_seq[:, 1:, :], output.unsqueeze(0).unsqueeze(2)), dim=1) print('Predicted values:', predictions) Explanation Model Definition: Line 9: self.fc = nn.Linear(hidden_size, output_size)Explanation: The fully connected layer outputs a single time step ahead. Line 13: out = self.fc(out[:, -1, :])Explanation: The model only uses the last time step’s hidden state to make a prediction. Training Loop: Loss Function: The model uses Mean Squared Error (nn.MSELoss) for regression tasks. Gradient Update: Gradients are calculated and applied via backpropagation (loss.backward() and optimizer.step()). Inference Loop: Line 45: input_seq = torch.cat((input_seq[:, 1:, :], output.unsqueeze(0).unsqueeze(2)), dim=1)Explanation: The previous input sequence is updated by dropping the oldest value and appending the new prediction, enabling iterative forecasting. — Part 2: Direct Multi-Step Forecasting Example: Input Sequence: [1, 2, 3] Target Sequence: [4, 5] (future values) Explanation: Multi-Step Prediction: The model is trained to predict multiple future time steps simultaneously. Final Hidden State Usage: It uses the final hidden state to directly predict all future values without iterative feedback. Key Difference: The output layer predicts all future steps at once, rather than one step at a time. PyTorch Code Example import torch import torch.nn as nn import torch.optim as optim # Define the RNN model for Direct Multi-Step Forecasting class DirectMultiStepRNN(nn.Module): def __init__(self, input_size, hidden_size, output_size, num_future_steps): super(DirectMultiStepRNN, self).__init__() self.rnn = nn.RNN(input_size, hidden_size, batch_first=True) # Output layer predicts multiple future steps self.fc = nn.Linear(hidden_size, output_size * num_future_steps) self.num_future_steps = num_future_steps self.output_size = output_size def forward(self, x, hidden): # Pass input through RNN layer out, hidden = self.rnn(x, hidden) # Use the final hidden state to predict future steps out = self.fc(out[:, -1, :]) # Only the final time step # Reshape output to (batch_size, num_future_steps, output_size) out = out.view(-1, self.num_future_steps, self.output_size) return out, hidden # Hyperparameters input_size = 1 # Feature dimension hidden_size = 10 # Number of hidden units output_size = 1 # Predicting one feature per step num_future_steps = 2 # Predicting two future steps learning_rate = 0.01 num_epochs = 100 # Training data x_train = torch.tensor([[[1.0], [2.0], [3.0]]]) # Shape: (batch_size,…
Iterative Forecasting which is Predicting One Step at a Time 2- Direct Multi-Step Forecasting with RNN 3- Seq2Seq Models for Time Series Forecasting – day 61