Core ML vs (PyTorch - TensorFlow)for deep learning integration on iOS app on Xcode using SWIFT

Core ML vs (PyTorch – TensorFlow)for deep learning integration on iOS app on Xcode using SWIFT

December 19, 2024
Posted by ingoampt

Core ML and Model Conversion

Abstract

Machine learning models are often developed using frameworks like PyTorch and TensorFlow, which offer dynamic graphing and flexibility. However, deploying these models on Apple devices requires their conversion to Core ML. This paper delves into the mathematical processes behind such conversions, emphasizing tensor format transformations, weight serialization, and graph representation. It also explores Core ML’s hardware optimizations, offering a complete understanding of the transformation process.

1. Introduction

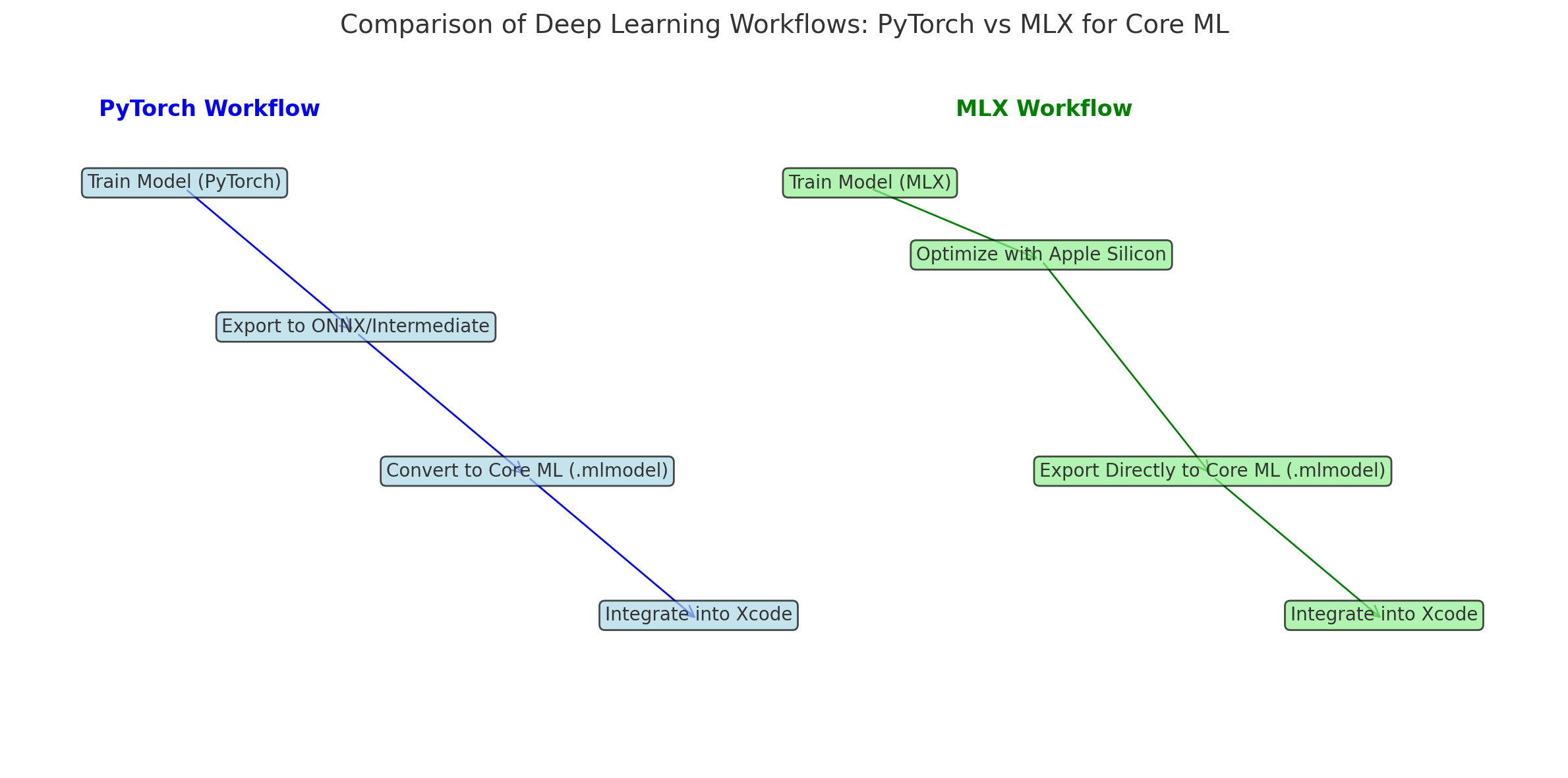
Core ML is Apple’s proprietary framework optimized for deploying machine learning models on iOS devices. Unlike PyTorch and TensorFlow, which prioritize training, Core ML is built for inference, utilizing Apple’s hardware to enhance performance.

Core ML requires models to be in a static computational graph format, necessitating mathematical transformations to ensure compatibility and accuracy. This paper provides insights into:

Tensor representations and operations.
Graph transformations (dynamic to static).
Optimizations specific to Core ML and Apple hardware.

—

2. Tensor Representations and Operations

2.1 Tensor Definitions

Tensors are generalizations of scalars, vectors, and matrices. They represent data in multi-dimensional arrays, crucial for neural network computations. A tensor is mathematically defined as:

$\mathcal{T} \in \mathbb{R}^{I_1 \times I_2 \times \cdots \times I_n}$

Where $I_1, I_2, \ldots, I_n$ are the dimensions of the tensor. For example:

A scalar is a 0-dimensional tensor.
A vector is a 1-dimensional tensor.
A matrix is a 2-dimensional tensor.

2.2 Tensor Operations

Neural networks heavily rely on tensor operations like addition and multiplication:

Tensor Addition: Adds tensors element-wise, assuming identical shapes:
$(\mathcal{A} + \mathcal{B})_{i_1, i_2, \ldots, i_n} = \mathcal{A}_{i_1, i_2, \ldots, i_n} + \mathcal{B}_{i_1, i_2, \ldots, i_n}$
Tensor Multiplication: Extends matrix multiplication across dimensions:
$(\mathcal{C})_{i,j} = \sum_k \mathcal{A}_{i,k} \cdot \mathcal{B}_{k,j}$

This forms the backbone of linear transformations in neural networks.

—

3. Computational Graphs

3.1 Static vs. Dynamic Graphs

Frameworks like PyTorch use dynamic graphs, building operations on-the-fly during execution. In contrast, Core ML relies on static graphs, where all operations are pre-defined. Static graphs enable greater optimization but reduce flexibility.

3.2 Graph Conversion

Converting a dynamic graph (PyTorch) to a static graph (Core ML) involves two key steps:

Tracing: Recording the model’s operations with sample data.
Freezing: Saving the computational graph with fixed parameters.

Mathematical representation of a linear layer:

$Y = XW + b$

Where:

$X \in \mathbb{R}^{N \times D}$ : Input tensor
$W \in \mathbb{R}^{D \times K}$ : Weight matrix
$b \in \mathbb{R}^K$ : Bias vector

—

4. Tensor Format Conversion

4.1 Format Differences

Tensors differ in layout conventions across frameworks:

**NCHW**: Batch size, channels, height, and width (PyTorch).
**NHWC**: Batch size, height, width, and channels (Core ML).

4.2 Permutation

To convert tensors from NCHW to NHWC, their axes are permuted:

$T'_{NHWC} = \text{Permute}(T_{NCHW}, [0, 2, 3, 1])$

Where $[0, 2, 3, 1]$ indicates the new axis order.

Example:

Input tensor: $T_{NCHW} \in \mathbb{R}^{1 \times 3 \times 224 \times 224}$

Output tensor: $T'_{NHWC} \in \mathbb{R}^{1 \times 224 \times 224 \times 3}$

—

5. Weight Serialization

5.1 Convolutional Layer Weights

Convolutional weights must be serialized to match Core ML’s requirements. PyTorch stores weights as:

$W \in \mathbb{R}^{F \times C \times K_H \times K_W}$

Core ML requires weights in:

$W' \in \mathbb{R}^{K_H \times K_W \times C \times F}$

5.2 Transposition

To convert weights, transpose the dimensions:

$W' = \text{Transpose}(W, [2, 3, 1, 0])$

—

6. Matrix Multiplications

6.1 Mathematical Definition

Matrix multiplication underpins fully connected layers. For matrices:

$A \in \mathbb{R}^{m \times n}$
$B \in \mathbb{R}^{n \times p}$

The product $C$ is:

$C_{i,j} = \sum_{k=1}^n A_{i,k} B_{k,j}$

6.2 Optimization

Core ML optimizes these multiplications using Apple’s Metal Performance Shaders (MPS), leveraging GPU parallelism.

—

Core ML and Model Conversion – Part 2

1. Detailed Tensor Format Conversion

1.1 Context of Conversion

Tensors in machine learning represent data as multi-dimensional arrays. Different frameworks use different formats for storing these arrays:

PyTorch: Uses the NCHW format (Batch Size, Channels, Height, Width).
Core ML: Requires the NHWC format (Batch Size, Height, Width, Channels).

1.2 Mathematical Representation

To convert tensors from NCHW to NHWC, we permute the axes:

$T'_{NHWC} = \text{Permute}(T_{NCHW}, [0, 2, 3, 1])$

This reorders the dimensions of the tensor. For example:

Input tensor in PyTorch:

$T_{NCHW} \in \mathbb{R}^{1 \times 3 \times 224 \times 224}$

After conversion to Core ML:

$T'_{NHWC} \in \mathbb{R}^{1 \times 224 \times 224 \times 3}$

1.3 Why This Matters

The reordering ensures compatibility with Core ML’s inference engine, which is optimized for the NHWC layout due to GPU hardware requirements.

—

2. Weight Serialization and Transformation

2.1 Weight Storage Formats

In convolutional layers, weights are stored as 4D tensors. The format varies by framework:

PyTorch: $W \in \mathbb{R}^{F \times C \times K_H \times K_W}$
Core ML: $W' \in \mathbb{R}^{K_H \times K_W \times C \times F}$

2.2 Transposing Weights

The weights must be transposed during conversion to match Core ML’s expected format:

$W' = \text{Transpose}(W, [2, 3, 1, 0])$

This ensures the convolution operation remains mathematically consistent.

2.3 Mathematical Proof of Consistency

The convolution operation is defined as:

$Y_{i,j,f} = \sum_{c=1}^{C} \sum_{k_h=1}^{K_H} \sum_{k_w=1}^{K_W} X_{i+k_h,j+k_w,c} \cdot W_{k_h,k_w,c,f} + b_f$

The transposition aligns the indices for the kernel dimensions and channels, ensuring the output remains accurate post-conversion.

—

3. Matrix Multiplications in Fully Connected Layers

3.1 Definition

Fully connected layers rely on matrix multiplication, which is mathematically defined as:

$C_{i,j} = \sum_{k=1}^{n} A_{i,k} \cdot B_{k,j}$

Where:

$A \in \mathbb{R}^{m \times n}$ : Input matrix
$B \in \mathbb{R}^{n \times p}$ : Weight matrix
$C \in \mathbb{R}^{m \times p}$ : Output matrix

3.2 Core ML Optimization

Core ML uses Metal Performance Shaders (MPS) to perform matrix multiplications efficiently by leveraging:

Parallelism across GPU cores.
Unified memory architecture to minimize memory transfer overhead.

3.3 Importance of Optimization

Matrix multiplication is computationally expensive with a time complexity of $O(n^3)$ . Optimizing this operation significantly reduces inference latency on Apple devices.

—

4. Non-Linear Activations

4.1 Swish Activation Function

The Swish activation function is mathematically defined as:

$\text{Swish}(x) = x \cdot \sigma(x), \quad \sigma(x) = \frac{1}{1 + e^{-x}}$

Core ML does not natively support Swish, requiring approximations.

4.2 Polynomial Approximation

A second-order polynomial can approximate Swish:

$\text{Swish}(x) \approx a_0 + a_1x + a_2x^2$

This approximation balances computational efficiency with accuracy.

—

5. Challenges in Model Conversion

5.1 Graph Translation

Dynamic graphs (used in PyTorch) must be converted to static graphs (used in Core ML). This involves tracing and freezing the model’s operations with sample data.

5.2 Numerical Precision

Core ML often uses $FP16$ (16-bit floating point) to improve performance during inference. Conversion from $FP32$ (32-bit floating point) involves rounding:

$x_{FP16} = \text{Round}(x_{FP32})$

5.3 Validation

Post-conversion validation ensures:

Accuracy of predictions is preserved.
Inference latency is reduced.

—

Conclusion

Core ML optimizes machine learning models for deployment on Apple devices through tensor format alignment, weight serialization, and hardware acceleration. Understanding these mathematical principles ensures successful model conversion and optimal performance.

Education