Activation Functions in Neural Networks: Why They Matter
Activation functions are pivotal in neural networks, transforming the input of each neuron to its output signal, thus determining the neuron’s activation level. This process allows neural networks to handle tasks such as image recognition and language processing effectively.
The Role of Different Activation Functions
Neural networks employ distinct activation functions in their inner and outer layers, customized to the specific requirements of the network:
- Inner Layers: Functions like ReLU (Rectified Linear Unit) introduce necessary non-linearity, allowing the network to learn complex patterns in the data. Without these functions, neural networks would not be able to model anything beyond simple linear relationships.
- Outer Layers: Depending on the task, different functions are used. For example, a softmax function is used for multiclass classification to convert the logits to probabilities that sum to one, which are essential for classification tasks.
Practical Application
Understanding the distinction and application of different activation functions is crucial for designing networks that perform efficiently across various tasks.
Building a Neural Network for Image Classification
This example demonstrates setting up a neural network in Python using TensorFlow/Keras, designed to classify images into three categories.
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Conv2D, MaxPooling2D
model = Sequential([
Conv2D(32, kernel_size=(3, 3), activation='relu', input_shape=(64, 64, 3)),
MaxPooling2D(pool_size=(2, 2)),
Conv2D(64, kernel_size=(3, 3), activation='relu'),
MaxPooling2D(pool_size=(2, 2)),
Flatten(),
Dense(128, activation='relu'),
Dense(3, activation='softmax')
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.summary()
The code above outlines each step in constructing the network, from input to output, detailing how each layer contributes to the task of image classification. The use of ‘relu’ in hidden layers and ‘softmax’ in the output layer optimizes the model for accuracy and efficiency.
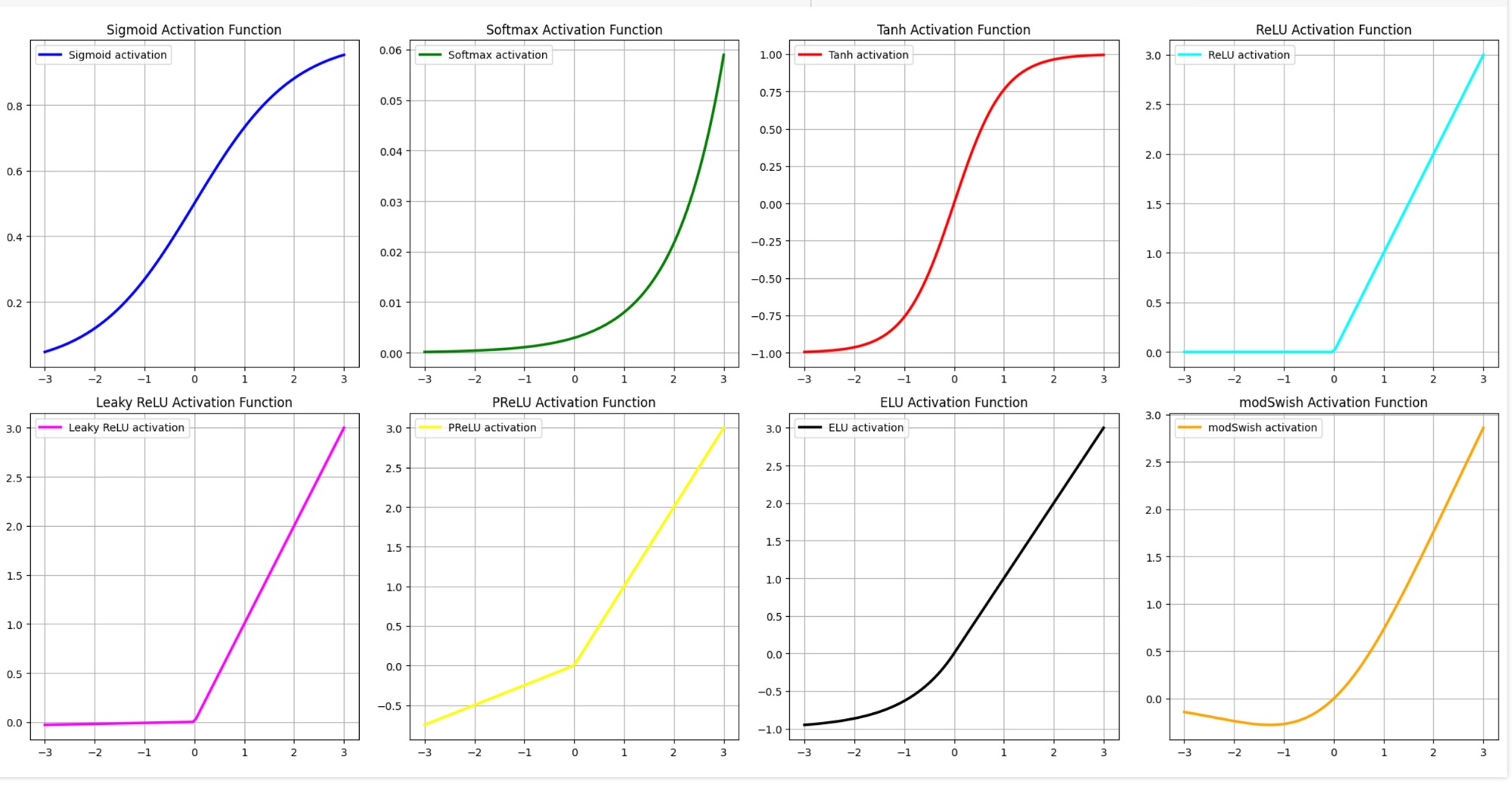
| Activation Function | Formula | Used in Layer | Purpose | Linearity |
|---|---|---|---|---|
| Sigmoid | $$\sigma(x) = \frac{1}{1 + e^{-x}}$$ | Output | Maps input to the range (0, 1), useful for binary classification. | Non-linear |
| Softmax | $$\text{Softmax}(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}}$$ | Output | Converts logits to probabilities for multiclass classification. | Non-linear |
| Tanh | $$\tanh(x) = \frac{e^x – e^{-x}}{e^x + e^{-x}}$$ | Hidden | Maps values between -1 and 1, zero-centered. | Non-linear |
| ReLU | $$f(x) = \max(0, x)$$ | Hidden | Replaces negative values with 0, allowing for faster convergence. | Non-linear |
| Leaky ReLU | $$f(x) = \max(0.01x, x)$$ | Hidden | Allows a small, non-zero output for negative inputs. | Non-linear |
| PReLU | $$f(x) = \max(\alpha x, x)$$ | Hidden | Parameter \(\alpha\) is learnable, improving learning dynamics. | Non-linear |
| ELU | $$f(x) = x \text{ if } x > 0 \text{ else } \alpha(e^x – 1)$$ | Hidden | Controls the vanishing gradient problem by outputting values below zero for negative inputs. | Non-linear |
| modSwish | $$f(x) = x \cdot \sigma(\beta x)$$ | Hidden | A modified version of Swish, continuously differentiable and non-monotonic. | Non-linear |